注:仅记录题目,后面必须回来做一遍
设f(x)=u(x)+v(x),g(x)=u(x)−v(x),并设limx→x0u(x)与limx→x0v(x)都不存在,则下列结论正确的是:
A. 若limx→x0f(x)不存在,则limx→x0g(x)必存在
B. 若limx→x0f(x)不存在,则limx→x0g(x)必不存在
C. 若limx→x0f(x)存在,则limx→x0g(x)必不存在
D. 若limx→x0f(x)存在,则limx→x0g(x)必存在
设函数f(x)=ex/(x−1)−11,则x=0是f(x)的第( )类间断点,x=1是f(x)的第( )类间断点
设函数f(x)=limn→∞1+x2n1+x,关于该函数的间断点,下列结论正确的是
A. 不存在间断点
B. 存在间断点x=1
C. 存在间断点x=0
D. 存在间断点x=-1
设f(x)=1+x2x,f1(x)=f[f(x)],f2(x)=f[f1(x)],fn+1(x)=f[fn(x)](n=1,2,3,⋯),则fn(x)=()
极限limx→∞(x−1x+2)x=?
设如下函数存在,[·]为取整函数,求I,a
I=x→0lim(ln(1+e1/x)ln(1+e2/x)+a[x])
已知limx→0xf(x)存在,且函数
f(x)=ln(1+x)+2x⋅x→0limsinxf(x)
,则limx→0xf(x)=___
n→∞lim(n+n−n−n)=
设下列极限存在且不为0,则常数k=___
n→∞limnk−(n−1)kn99
设函数f(x)在[a,b]上连续,x1,x2,⋯,xn是[a,b]上的一个点列,求下列极限
n→∞limnn1k=1∑nef(xk)
单调有界准则
设x1=2,xn+(xn−4)xn−1=3 (n=2,3,...),证明limn→∞xn存在,并求其值
当n→∞时,(1+n1)n−e与na是等价无穷小量,则a=___
设单调递减数列{xn}满足xn+1=2ln(1+xn),x1>a>0,且a是x−2ln(1+x)=0的唯一非零解,证明{xn}收敛
设f(x)满足f(0)=0,且f′(x)存在,求:
x→0limln(1−xsinx)f(1−cosx)
设f(x)=⎩⎨⎧xxsinxπ,A,ax2+b,x<0x=0x>0,求常数A,a,b的值,使f(x)在x=0处可导,并求f′(x)
已知函数f(x)在x=1处可导,且limx→0x2f(ex2)−3f(1+sin2x)=2,求f′(1)
设δ>0,f(x)在[−δ,δ]上有定义,f(0)=1,且满足
x→0limx2ln(1−2x)+2xf(x)=0
证明:f(x)在x=0处可导,并求f′(0)
泰勒公式
设函数f(x)连续,limx→1lnxf(x)−1=2,则曲线y=f(x)在点x=1处的切线方程是
已知f′(x)=Aex(A为常数),则f(x)的反函数的二阶导数为___
错误原因:计算错误
设函数y=y(x)由⎩⎨⎧x=ln(1+t2)+1y=2arctant−(t+1)2确定,则dx2d2y=___
错误原因:计算错误
设y=sin4x+cos4x,则当n≥1时,y(n)(x)=___
错误原因:无从下手
设y=y(x)是由方程sin(xy)=lnyx+e+1确定的隐函数,求y′(0)的值
错误原因:计算错误
已知g(x)在x=0处二阶可导,且g(0)=g′(0)=0,设
f(x)=⎩⎨⎧xg(x),0,x=0x=0
证明:f(x)的导函数在x=0处连续
错误原因:无从下手
设f(x)=x2,h(x)=f[1+g(x)],其中g(x)可导,且g′(1)=h′(1)=2,则g(1)=
错误原因:计算错误
设f(x)=(lnx−1)(ln2x−2)⋯(lnnx−n),n≥2,则f′(e)=___
错误原因:计算错误
已知函数f(x)=x2ln(2−x),则当n≥3时,f(n)(0)=___
错误原因:遗忘公式,无从下手
曲线y=(x−5)x32的拐点坐标为___
错误原因:计算错误
求曲线y=f(x)=xex21的渐近线
错误原因:粗心,计算错误
设f(x)=3x2+Ax−3,问正数A至少为何值时,可使对任意的x∈(x,+∞),都有f(x)≥20成立
错误原因:计算错误
函数y=ex+2e−x的最小值为___
错误原因:计算错误
已知函数y=f(x)连续,其二阶导函数的图像如图所示,则y=f(x)的拐点个数为__

错误原因:忽略定义
曲线y(x)=ln∣e2x−1∣的斜渐近线为___
错误原因:无从下手
曲线x2−xy+y2=1在点(1,1)的曲率为___
错误原因:公式套错了
已知曲线y=f(x)在其点(0,1)处的曲率圆方程为(x−1)2+y2=2,且当x→0时,二阶可导函数f(x)与a+bx+cx2的查为o(x2),则a=___,b=___,c=___
错误原因:蒙的不算
设实数a0,a1,a2,⋯,an满足a0+2a1+3a2+⋯n+1an=0,证明方程:
a0+a1x+a2x2+⋯+anxn=0
在(0,1)内至少有一个根
错误原因:无从下手
已知f(x)在[0,1]上连续,在(0,1)内可导,且f(0)=0,f(1)=1,证明:
存在ξ∈(0,1),使得f(ξ)=1−ξ
存在η,τ∈(0,1),η=τ,使得f′(η)f′(τ)=1
错误原因:第二题无从下手
设函数f(x)在[0,1]上二阶可导,且f(0)=f(1)=0,x∈[0,1]min{f(x)}=−1,证明:存在ξ∈(0,1),使得f′′(ξ)≥8
错误原因:自己做一遍
设当x>0时,方程kx+x21=1有且仅有一个根,求k的取值范围
错误原因:粗心
设存在0<θ<1,使得arcsinx=1−(θx)2x,−1≤x≤1,则x→0limθ=___
错误原因:这什么玩意?
设函数f(x)可导,且∣f′(x)∣≤1,f(0)=1,证明∣f(x)∣≤1+x,0<x<1
错误原因:遗忘定义,无从下手
将sinx在x=0处展开成一阶带拉格朗日余项的泰勒公式
证明∣xsinx−1∣≤21∣x∣,x=0
错误原因:无从下手
当0<x<2π时,证明sinx>π2x
设数列{xn},{yn}满足xn+1=sinxn,yn+1=yn2,n=1,2,3,⋯, x1=y1=21,当n→∞时,证明:yn是比xn高阶的无穷小量
错误原因:太大了,无从下手
设数列{xn}满足:0<xn<2π, xncosxn+1=sinxn, n=1,2,⋯,证明{xn}收敛,并求n→∞limxn
甲车以24km/h的速度向北行驶,同时正东10km处乙车以20km/h的速度向东行驶,从这一时刻起经过1小时后,求两车之间的距离对时间的变化率
错误原因:图没画好
已知某圆柱底面半径与高随时间变化的速率分别为2cm/s,-3cm/s,且圆柱体的体积与表面积随时间变化的速率分别为−100πcm3/s,40πcm2/s,则圆柱体的底面半径与高分别为?
答案蒙对了,但还是想自己算
我服了爸爸
n→∞limi=1∑nn+i1sinniπ=?
讨论∫2+∞xlnpx1dx的敛散性,其中p为任意实数
n→∞limn1i=1∑n[ln(3n−2i)−ln(n+2i)]=?
已知下式,则()
M=∫−2121(1+1+x2x)dx,N=∫01x2(1+x)ln2(1+x)dx,K=∫011+xexdx
(A). M>N>K
(B). N>K>M
(C). K>M>N
(D). K>N>M
错误原因:什么√8
设函数g(x)在[0,π2]上连续,若在(0,π2)内有g′(x)≥0,则对任意的x∈(0,π2),都有()
(A). ∫xπ2g(t)≥∫xπ2g(sint)dt
(B). ∫x1g(t)≤∫x1g(sint)dt
(C). ∫x1g(t)≥∫x1g(sint)dt
(D). ∫xπ2g(t)≤∫xπ2g(sint)dt
若1−x2是xf(x)的一个原函数,则∫01f(x)1dx=?
已知函数f是∫1ex1+t31dt的反函数,则f′(0)=?
已知:
∫xf(x)dx=arcsinx+C
求:
∫f(x)1dx
x→+∞limeex∫ex(1−t1)t⋅eetdt=?
∫arcsina+xxdx=?
∫xarctanexdx=?
∫043π1+cos2x1=?
∫21232x−x2(1−x)arcsin(1−x)dx=?
∫−4π4πe2xcosxcosx−sinxdx
∫0π1+cos2xxsinxdx
∫−111+3x2x+1dx
已知
f(x)=⎩⎨⎧1+sinx1,1+ex1,x≥0.x<0
求下式
∫−14πf(x)dx
求连续函数f(x),使其满足:
∫01f(tx)dt=f(x)+xsinx
设f(x)=∫01t∣t−x∣dt,求f′(x)
计算下列不定积分
∫secxdx
∫sec3xdx
∫csc3xdx
∫tan3xdx
∫sin2x1dx
∫a+bcosx1dx
∫a+bsinx1dx
∫01e−xdx=?
∫04πsec3θdθ
设连续函数f(x)满足f(x+1)−f(x)=xlnx,∫01f(x)dx=0,则∫12f(x)dx=?
设y=1+x2x,则
∫2123xydy=?
若e−x是f(x)的一个原函数,则
∫12x21f(lnx)dx=?
若函数f(x)连续,g(x)=∫02xf(x+2t)dt,则当x→0+时,g(x)是x的__
A. 高阶无穷小
B. 低阶无穷小
C. 等价无穷小
D. 同阶非等价无穷小
设f(x)在[−a,a]上是连续的偶函数,a>0,g(x)=∫−aa∣x−t∣⋅f(t)dt,则在[−a,a]上___
A. g(x)是单调递增函数
B. g(x)是单调递减函数
C. g(x)是偶函数
D. g(x)是奇函数
若F(x)=∫−ππ∣x−t∣sintdt,则F′(0)=?
若函数y(x)=∫2x2e−tdt,则
dx2d2[y(x)]∣x=−1=?
设an=∫01xn1−x2dx,则
n→∞lim(an−2an)n=?
∫−∞+∞∣x∣e−x2dx=?
双纽线(x2+y2)2=x2−y2所围成的区域的面积用定积分表示为___
圆域x2+(y−b)2≤k2(0<k<b)绕x轴旋转一周所得旋转体的体积为
星形线x=cos3t,y=sin3t(0≤t≤2π)的弧长为___
已知曲线y=ax(a>0)与曲线y=lnx在点(x_0,y_0)处有公共切线,求:
常数a及切点(x0,y0)
计算由摆线{x=a(t−sint),y=a(1−cost)(a>0,0≤x≤2π)与x轴所围平面图形绕y轴旋转一周所得旋转体的体积
求曲线y=3−∣x2−1∣与x轴围成的封闭图形绕直线y=3旋转一周所得旋转体的体积
曲线y=x2+4x+51与x轴在区间(0,+∞)上所围成的图形面积为
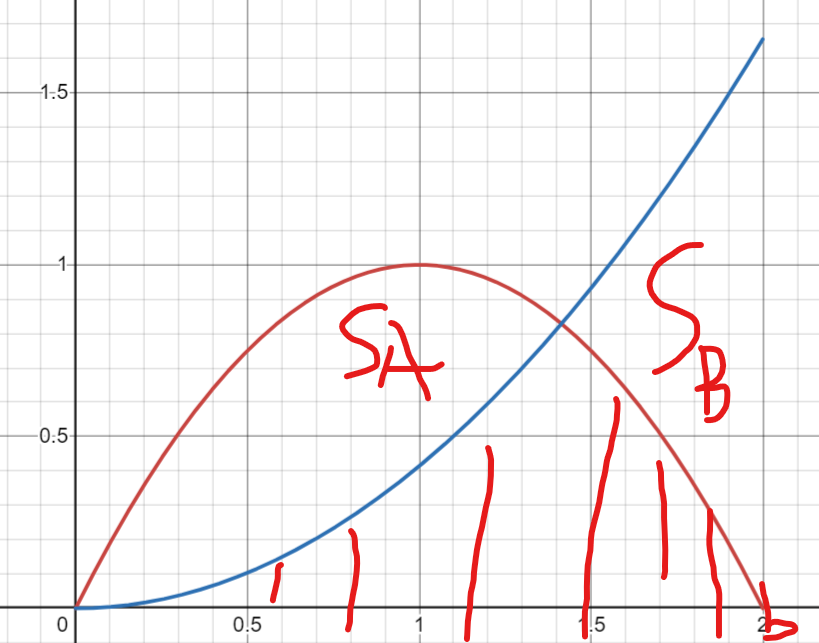
如图所示,抛物线y=(2−1)x2把y=x(b−x)(b>0)与x轴所围成的闭区域分为面积为SA与SB的两部分,则
A. SA<SB
B. SA=SB
C. SA>SB
D. SA,SB与B的数值无关
过点(p,sinp)作曲线y=sinx的切线,设该曲线与切线及y轴所围成图形的面积为S1,曲线与直线x=p及x轴所围成的图形面积为S2,则
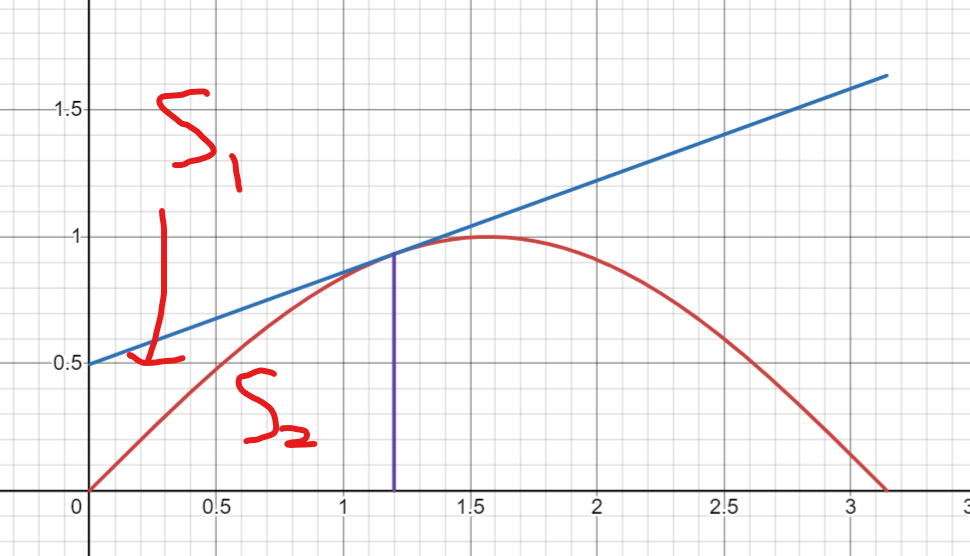
p→0+limS1+S2S2=?
设f(x)具有二阶连续导数,若曲线y1=f(x)过点(0,0),且与曲线y2=ax(a>1)在点(1,a)处相切,∫01xf′′(x)dx=2ln2−2,则a=?
已知函数f(x)=x∫1xtet2dt,则f(x)在(0,1)上的平均值为
已知曲线L:y=e−x(x≥0),设P是L上的动点,V是L上从点A(0,1)到点P的一端弧绕x轴旋转一周所得的旋转体体积,当P运动到点(1,e1)时,设x轴正向的速度为1,求此时V关于时间t的变化率
曲线y=lnsinx(6π≤x≤3π)的弧长为
已知函数y=y(x)由方程y4−6xy+3=0(1≤y≤2)所决定,则曲线y=y(x)从点(32,1)到点(1219,2)的长度为?



