10.1 一元函数积分学的几何应用

提示

前提：本章的曲线都是连续曲线

本章核心：套公式，做计算

1. 计算平面图形的面积

提示

三大体系下的图形：

1. 直角坐标系下：直接算
2. 参数方程下：直接算(少)、换元法
3. 极坐标系下：直接算

1. 曲线$y=y_1(x)$与$y=y_2(x)$及$x=a,x=b(a<b)$所围成的平面图形的面积：

$$S=\int_a^b|y_1(x)-y_2(x)|dx$$

2. 曲线$r=r_1(θ)$与$r=r_2(θ)$与两射线$θ=\alpha,\theta=\beta(0<\beta-\alpha\leq2π)$所围成的曲边扇形的面积为：

$$S=\frac 12\int_\alpha^\beta|r_1^2(\theta)-r_2^2(\theta)|d\theta$$

提示

可以将这个公式理解为，对曲边扇形以原点射线为界做微分

也就是，近似成多个三角形相加的情况

而又有$dl=r·\sin d\theta\backsim r·d\theta$

所以由三角形的公式，得到$\frac 12r·dl\backsim\frac 12 r^2·d\theta$

关于参数方程的代换

有$y=f(x)=f(x(t))=y(t)$

参数方程换元：令$x=x(t)$

时刻牢记！

2. 计算旋转体的体积

1. 曲线$y=y(x)$与$x=a,x=b(a<b)$及x轴围成的曲边梯形绕x轴旋转一周所得到的旋转体的体积

$$V_x=\int_a^bπy^2(x)dx$$

巧记

即，把$y(x)$看成r，微分成每一个圆，进行求和

2. 曲线$y=y(x)$与$x=a,x=b(0\leq a<b)$及x轴围成的曲边梯形绕y轴旋转一周所得到的旋转体的体积

$$V_y=2π\int_a^bx|y(x)|dx$$

巧记

即，把旋转体微分成多个圆环，每个环的底边周长是$2\pi x$，高是$|y(x)|$

而这个圆环体的底边"宽"就是$dx$

3. 平面曲线绕定直线旋转

设平面曲线$L: y=f(x),a\leq x\leq b$，且$f(x)$可导(这是要转的曲线)

设直线$L_0:Ax+By+C=0$，且过$L_0$的任一条垂线与L至多有一个交点，则L绕$L_0$旋转一周所得旋转体的体积为

$$V=\frac{\pi}{(A^2+B^2)^{3/2}}\int_a^b[Ax+Bf(x)+C]^2|Af'(x)-B|dx$$

若$L_0\Rightarrow y=0$(x轴)，则有

$$V_x=\int_a^bπy^2(x)dx$$

3. 计算函数的平均值

设$x∈[a,b]$，函数$y(x)$在$[a,b]$上的平均值为

$$\bar{y}=\frac{1}{b-a}\int_a^by(x)dx$$

4. 其他几何应用

1. 平面上的曲边梯形的形心坐标公式

$$\bar{x}=\frac{\int_a^bxf(x)dx}{\int_a^bf(x)dx}$$

$$\bar{y}=\frac{\frac 12\int_a^bf^2(x)dx}{\int_a^bf(x)dx}$$

2. 平面曲线的弧长

1. 直角坐标系

$$s=\int_a^b\sqrt{1+[y'(x)]^2}dx$$

2. 参数方程

$$s=\int_\alpha^\beta\sqrt{[x'(t)]^2+[y'(t)]^2}dt$$

3. 极坐标系

$$s=\int_\alpha^\beta\sqrt{[r(\theta)]^2+[r'(\theta)]^2}d\theta$$

速记：r方加r导方

3. 旋转曲面的侧面积

提示

即一个硬币的厚度(ds)乘以周长

ds就是弧长的微分啦！

算体积可以用dx，但是算面积必须要用ds，否则累加后会出现有限误差

1. 曲线L由直角坐标系确定，绕x轴旋转一周所得旋转曲面的面积为

$$S=2\pi\int_a^b|y|ds=2π\int_a^b|y|\sqrt{1+[y'(x)]^2}dx$$

2. 曲线L由参数方程确定，绕x轴旋转一周所得旋转曲面的面积为

$$S=2π\int_\alpha^\beta|y(t)|ds=2π\int_\alpha^\beta|y(t)|\sqrt{[x'(t)]^2+[y'(t)]^2}dt$$

3. 曲线L由极坐标系确定，绕x轴旋转一周所得旋转曲面的面积为

$$S=2π\int_\alpha^\beta|r(\theta)\sin\theta|ds=2π\int_\alpha^\beta|r(\theta)\sin\theta|\sqrt{[r(\theta)]^2+[r'(\theta)]^2}d\theta$$

4. 平行截面面积为已知的立体体积

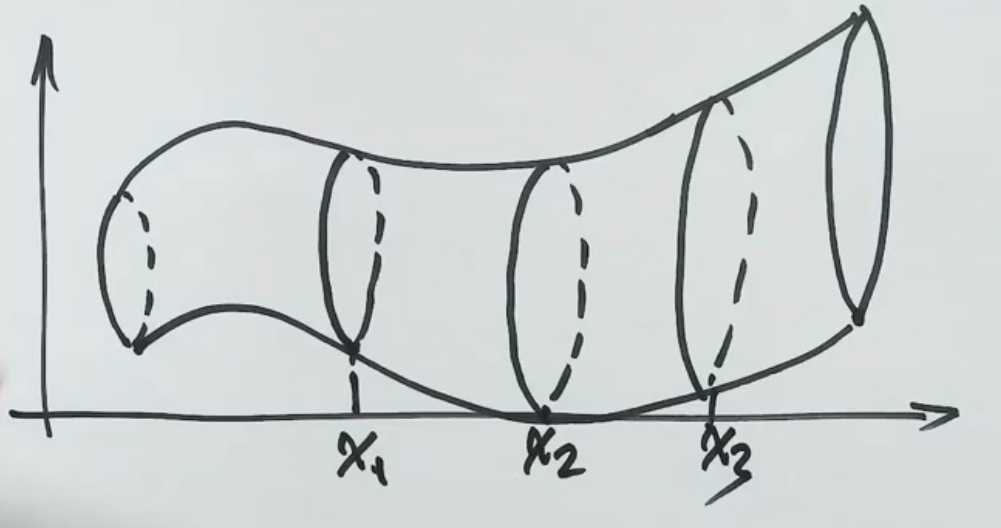
在区间$[a,b]$上，垂直与x轴的平面截立体$\Omega$所得到的截面面积为x的连续函数$A(x)$，则$\Omega$的体积为

$$V=\int_a^bA(x)dx$$