12.1 一元函数积分学的物理应用

1. 变力沿直线做功

设方向沿x轴正向的力函数为$y=F(x)(a\leq x\leq b)$(变力)，则物体沿x轴从点a移动到点b时，变力$F(x)$所做的功为

$$W=\int_a^bF(x)dx$$

功的微元$dW=F(x)dx$

注意：有些会说成阻力，打进去的力就是克服阻力做功

2. 抽水做功

将容器内的水全部抽出所做的功为

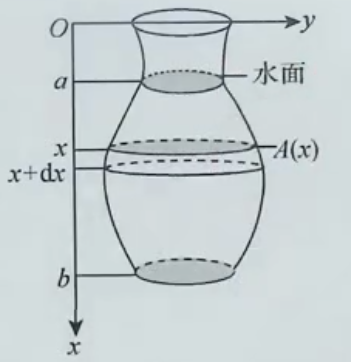容器

$$W=\rho g\int_a^bxA(x)dx$$

$\rho$为水的密度，$g$为重力加速度

功的微元$dW=\rho g xA(x)dx$为位于x处厚度为dx，水平截面面积为$A(x)$的一层水被抽出(路程为x)所做的功

3. 静水压力

垂直浸没在水中的平板ABCD的一侧受到的水压力为

$$P=\rho g\int_a^bx[f(x)-h(x)]dx$$

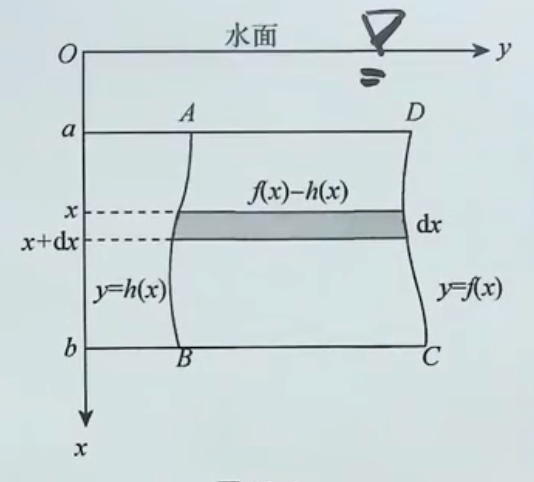
压力微元$dP=\rho gx[f(x)-h(x)]dx$，即图中矩形条受到的压力，x表示水深，$f(x)-h(x)$是矩形条的宽度，dx是矩形条的高度