14.2 二重积分的计算

1. 直角坐标系下的计算方法：

图

口诀：

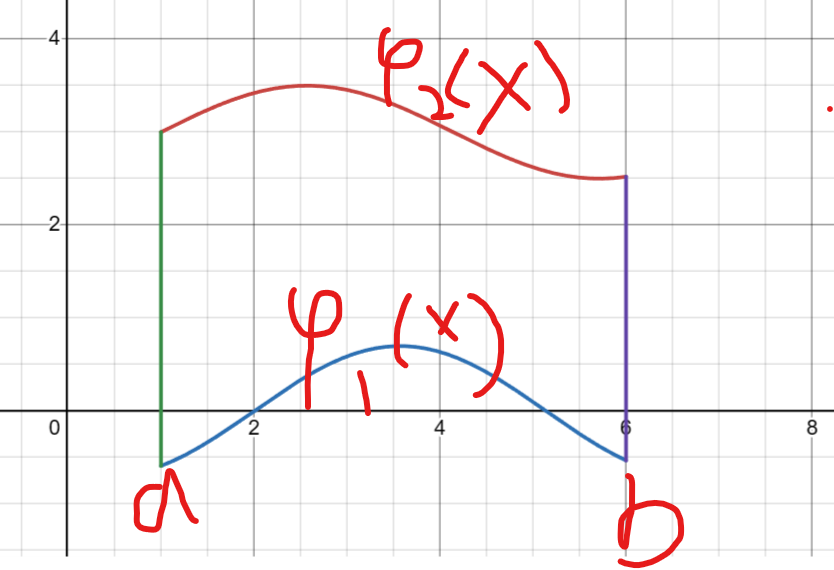
• 后积先定限：靠前(更好定上下限)的积分的变量上下限先定好，如图中先定a,b
• 限内画直线：对定限的坐标轴从零出发往正方向画一条线
• 先交写下限：直线第一个接触的函数为下限
• 后交写上限：直线第二个接触的函数为上限

$$\iint\limits_Df(x,y)d\sigma=\int_a^bdx\int_{\varphi_1(x)}^{\varphi_2(x)}f(x,y)dy$$

其中D为X型区域：$φ_1(x)\leq y\leq φ_2(x),a\leq x\leq b$

$$\iint\limits_Df(x,y)d\sigma=\int_c^ddy\int_{\psi_1(y)}^{\psi_2(y)}f(x,y)dx$$

其中D为Y型区域：$\psi_1(x)\leq x\leq \psi_2(x),c\leq y\leq d$

二重积分计算的注意事项

1. 积分的微元无论如何，必须为正
2. 积分的上下限必须下限小于上限，警惕题目倒置。当出现倒置的情况时，需要交换上下限并添负号
3. 计算二重积分的关键是确定积分限，为此，要画好积分区域D的边界图形。当D的边界图形不易画出时，要写出D的不等式的表达式
4. 在计算完其中一重积分后，写入上下限时，最好写明谁等于谁，避免出现变量代错的情况

交换积分次序

有时候，会出现原积分难以积分的情况，此时需要做交换积分次序，步骤如下

1. 还原积分区域
2. 交换积分次序

提示

书P252 没有初等函数形式的原函数，需要交换积分次序

当$x\to0$时，$\int_0^x(1-\cos t)dt\sim\int_0^x\frac 12t^2dt$

意思是，如果被积函数可以做无穷小替换时，可以直接不求导，如此这般积分等价代换

2. 极坐标系的积分方法

极坐标系下，有：

$$\begin{cases} x=r\cos\theta\\ y=r\sin\theta \end{cases}$$

则有

$$dxdy=\color{red}{r}drd\theta$$

积分有三种情况：

$$\iint\limits_Df(x,y)d\sigma=\begin{cases} \int_\alpha^\beta d\theta\int_{r_1(\theta)}^{r_2(\theta)}f(r\cos\theta,r\sin\theta)rdr&\text{(极点O在区域D外部)}\\\\ \int_\alpha^\beta d\theta\int_0^{r(\theta)}f(r\cos\theta,r\sin\theta)rdr&\text{(极点O在区域D边界)}\\\\ \int_0^{2\pi} d\theta\int_0^{r(\theta)}f(r\cos\theta,r\sin\theta)rdr&\text{(极点O在区域D内部)} \end{cases}$$

极坐标系和直角坐标系选择的一般原则

主要看(1)

如果给出一个二重积分：

(1) 看被积函数是否符合$f(x^2+y^2),f(\frac yx),f(\frac xy)$等形式

(2) 看积分区域是否为圆或者为圆的一部分

如果是，则考虑使用极坐标系。否则，优先考虑使用直角坐标系

积分次序

先积r，后积θ

因为通常来说，θ更好定限

极坐标系和直角坐标系的相互转换

一是用好$\begin{cases} x=r\cos\theta\\ y=r\sin\theta \end{cases}$这个公式；二是画出积分区域D的边界图形，做好上下限的转换

3. 二重积分下的换元法

牢记换元有三换：积分上下限、被积函数、面积元素

• $f(x,y)\to f[x(u,v),y(u,v)]$

• $\iint\limits_{D_{xy}}\to\iint\limits_{D_{uv}}$

• $dxdy\to \left|\frac{\partial(x,y)}{\partial(u,v)}\right|dudv$

其中

$$\frac{\partial(x,y)}{\partial(u,v)}=\begin{vmatrix} \frac{\partial x}{\partial u} & \frac{\partial x}{\partial v}\\\\ \frac{\partial y}{\partial u} & \frac{\partial y}{\partial v} \end{vmatrix}\not=0$$

称为J行列式