13.2 多元函数微分法则

1. 链式求导法则

设$z=f(u,v)$，$u=\varphi(x,y)$，$v=\psi(x,y)$，则$z=f[\varphi(x,y),\psi(x,y)]$，且

$$\frac{\partial z}{\partial x}=\frac{\partial z}{\partial u}·\frac{\partial u}{\partial x}+\frac{\partial z}{\partial v}·\frac{\partial v}{\partial x}\\\\\space\\\\\frac{\partial z}{\partial y}=\frac{\partial z}{\partial u}·\frac{\partial u}{\partial y}+\frac{\partial z}{\partial v}·\frac{\partial v}{\partial y}$$

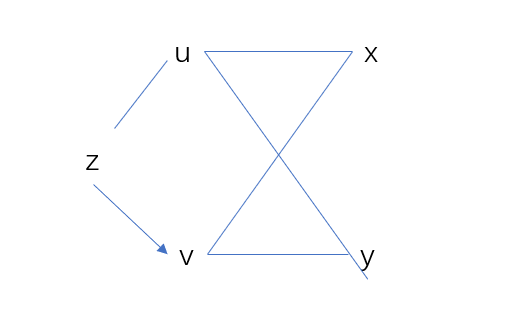可复合成该图的形式

若最终变量只有一个时

设$z=f(u,v)$，$u=\varphi(t)$，$v=\psi(t)$，则$z=f[\varphi(t),\psi(t)]$，且

$$\frac{dz}{dt}=\frac{\partial z}{\partial u}·\frac{du}{dt}+\frac{\partial z}{\partial v}·\frac{dv}{dt}$$

此处是全导数，因为最后的变量只有t一个

注意

注意：$\frac{\partial z}{\partial u}$是把u看成整体求导而与u的值无关，u的值在后面！

也就是说，这里是对位置求导，而不是对值求导

提示

无论z对哪个变量求导，也无论z求了几阶导，求导后的新函数(如$f_1',f_2'$)仍然具有与原函数完全相同的复合结构

提示

对位置求导时，常用数字表示位置

例如$f_1'(0,0)$

题目有时候也会写成$f_x'$，要注意这里仍然是对位置求导的函数

2. 全微分形式不变性

设$z=f(u,v)$，$u=u(x,y)$，$v=v(x,y)$，如果$z=f(u,v)$，$u=u(x,y)$，$v=v(x,y)$分别有连续偏导数，则复合函数$z=f(u,v)$在$(x,y)$处的全微分仍可表示为：

$$dz=\frac{\partial z}{\partial u}du+\frac{\partial z}{\partial v}dv$$

即无论u,v时自变量还是中间变量，上式总成立

3. 隐函数存在定理

定理1

对于由方程$F(x,y)=0$确定的隐函数$y=f(x)$，当$F_y'(x,y)\not=0$时，则有

$$\frac{dy}{dx}=-\frac{F_x'(x,y)}{F_y'(x,y)}$$

提示

也可以简写成

$$\frac{dy}{dx}=-\frac{F_x'}{F_y'}$$

注意：这个一样适用于一元函数的隐函数，可以用！

或者说就是一元函数的隐函数吧。。

定理2

对于由方程$F(x,y,z)=0$确定的隐函数$z=f(x,y)$，当$F_z'(x,y,z)\not=0$时，则有

$$\frac{\partial z}{\partial x}=-\frac{F_x'(x,y,z)}{F_z'(x,y,z)}\text{，}\frac{\partial z}{\partial y}=-\frac{F_y'(x,y,z)}{F_z'(x,y,z)}$$

提示

若$F_z'(x,y,z)=0$，则无法确定偏导数，但仍可能存在