1.1 函数的概念与特性

基础知识结构(要之后能自己画)

函数 $y=f(x)$

反函数 $y=f^{-1}(x)$

复合函数 $y=f[g(x)]$

隐函数

四种特性：

• 有界性
• 单调性
• 奇偶性
• 周期性

函数图像：

• 基本初等函数与初等函数
• 分段函数

函数

x 自变量

y 因变量

D 定义域

则有

$$y=f(x) \space\space x∈D$$

每一个x都有且只有一个对应的y值与其对应

$$\text{值域：}f(x)|x∈D$$

上述定义的函数是单值函数

一对一(y=x)，多对一(y=x²)，都是单值函数

但是一个x对应多个y，即一对多，那叫多值函数(y²=x)

一般来说，函数默认是单值函数

一句话：数与形，铅锤划线法——作任意一条铅垂直线(垂直于x轴 )

若任意一条铅垂直线与f(x)至多有一个交点，则f(x)为单值函数

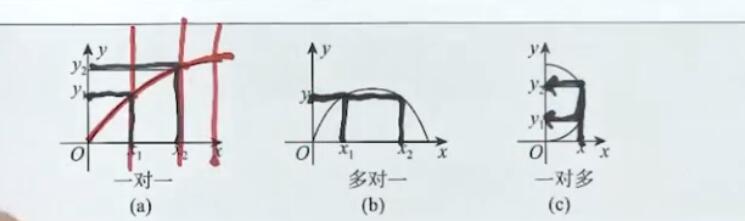
(记得看例题1.1和1.2)

反函数

必须要符合铅锤划线法，即必须要单值函数，才能找到反函数

直接将函数y=f(x)的x挪到一边，变成x=φ(y)，即y=f(x)的反函数，一般记作x=f^-1(y)

相对反函数来说，原来的函数称为直接函数

有两点需要注意：

1. 严格单调函数必有反函数

2. 若把x=f^-1(y)和y=f(x)的图像画在同一坐标系中，则它们完全重合，只有把x=f^-1(y)反写成y=f^-1(x)，它们的图像才会关于y=x对称

水平划线法：符合铅锤划线法的条件下，垂直于y轴作水平直线，若至多一个交点，则有反函数

巧记

铅垂直线定单多(单值函数、多值函数)

水平直线定反直(反函数、直接函数)

记得看30讲P4下面的注解

复合函数

y=f[g(x)](x∈D)

确定的函数称为由u=g(x)和函数y=f(x)构成的复合函数，u称为中间变量

解题时，需要注意u的定义域和值域，套到f(x)上时都有用

隐函数

设方程$F(x,y)=0$，当x取某区间内的任意值时，总有满足该方程的唯一值y存在，则称$F(x,y)=0$在上述区间内确定了一个隐函数$y=y(x)$

例如，$x+y^3-1=0$确定了一个隐函数，可以被显化为$y = \sqrt[3]{1-x}$

$\sin(xy) = \ln\left(\frac{x+e}{y}\right) + 1$也确定了一个隐函数，但是不易显化

一般来说，由$F(x,y)=0$所确定的隐函数求y(x₀)，若代入$x_0$易求出$y(x_0)$，则直接求之；若不易求出y(x₀)，则用观察法，例如：

① 设函数$y=y(x)$由方程$lny-\frac{x}{y}+y=0$确定，当$x=2$时，$y(2)=1$

② 设函数$y=y(x)$由方程$lny+e^y-1= \frac{x}{2}$确定，当$x=2$时，$y(2)=1$

函数的四种特性

有界性

在几何上看，在给定的区间，函数y=f(x)能够被两条直线y=|M|“完全包起来”，则为有界

如果这样的M不存在，就称f(x)在I上无界

※ 从解析上来说，如果找到某个正数M，使得$|f(x)|\leq M$，则为有界

有界和无界的讨论首先要指明区间I，比如$y=\frac{1}{x}$在$(2, + \infty$)内有界，但是在$(0,2)$之间无界

注意$x^2 = |x^2| = |x|^2$，$|x|=\sqrt{x^2}$

基本不等式：详见30讲的P52

$$\frac{2}{\frac{1}{a}+\frac{1}{b}} < \sqrt{ab} < \frac{a+b}{2} < \sqrt{\frac{a^2+b^2}{2}}$$

单调性

单增、单减

任选两点，恒有大于或小于，则有单调性

定义法很重要

试题中常用到如下定义法的判别形式

对于任意$x_1,x_@∈D，x_1\not=x_2,$有

$$f(x)\text{是单调增函数}\iff(x_1-x_2)[f(x_1)-f(x_2)]>0$$

$$f(x)\text{是单调减函数}\iff(x_1-x_2)[f(x_1)-f(x_2)]>0$$

$$f(x)\text{是单调不减函数}\iff(x_1-x_2)[f(x_1)-f(x_2)]\geq0$$

$$f(x)\text{是单调不增函数}\iff(x_1-x_2)[f(x_1)-f(x_2)]\leq0$$

奇偶性

※ 非常重要

$f(-x)=f(x)$，则偶函数

$f(-x)=-f(x)$，则奇函数

偶函数的图像关于y轴对称

奇函数的图像关于原点对称

注意：上述定义的定义域必须关于原点对称

注

$f(x)+f(-x)$必是偶函数

$f(x)-f(-x)$必是奇函数

对于任一函数$f(x)$，令$u(x)=\frac{1}{2}[f(x)+f(-x)],v(x)=\frac{1}{2}[f(x)-f(-x)]$，则$u(x)$为偶函数，$v(x)$为奇函数

由

$$f(x)=\frac{1}{2}[f(x)+f(-x)]+\frac{1}{2}[f(x)-f(-x)]=u(x)+v(x)$$

※ 可知任意一个函数都可以写成一个奇函数与一个偶函数之和的形式

这个很重要！！

对于复合函数来说

$$f[φ(x)]$$

有：内偶则偶，内奇同外

奇[偶]->偶，如$sinx^2$

偶[奇]->偶，如$cos(sinx),|sinx|$

奇[奇]->奇，如$sin\frac{1}{x},\sqrt[3]{tanx}$

偶[偶]->偶，如$cos|x|,|cosx|$

非奇非偶[偶]->偶，如$e^{x^2},ln|x|$

4. 一个特色：

$$[ln(x+\sqrt{x^2+1})]'=\frac{1}{\sqrt{x^2+1}}$$

奇函数求导必是偶函数

偶函数求导必是奇函数

前提都是可导

$$f(x)\text{奇}\rightarrow\int_0^x{f(t)}{\rm d}t \text{偶}$$

(奇偶互换成立)

见例9.23

设对任意的x,y，都有$f(x+y)=f(x)+f(y)$，则$f(x)$是奇函数

提示

形如$\frac{1}{a^x+1}-\frac{1}{2}\space(a>1)$的函数也是奇函数

详见：1000题A1.6

提示

对于$\lim_{-\infty}^{+\infty}f(x)$来说，不能将上下区间视为对称区间，因为是无穷区间

除非两侧极限均收敛，此时可视作对称区间

周期性

对于任意$x∈D$，有$x\pm T∈D$，且$f(x+T)=f(x)$，则称$f(x)$为周期函数，T称为$f(x)$的周期

重要结论

1. 若$f(x)$以T为周期，则$f(ax+b)$以$\frac{T}{|a|}$为周期
2. 若$g(x)$为周期函数，则$f[g(x)]$也是周期函数
3. ※ 若$f(x)$是以T为周期的可导函数，则$f'(x)$也以T为周期，见例3.1
4. ※ 若$f(x)$是以T为周期的连续函数，则只有在$\int_0^Tf(x){\rm d}x=0$时，$\int_0^xf(t){\rm d}t$也以T为周期，见9.25