y=A,A为常数,其图形为平行于x轴的水平直线
偶函数
易考"找交点个数"或在概率论中求概率P{g(X)≤y}
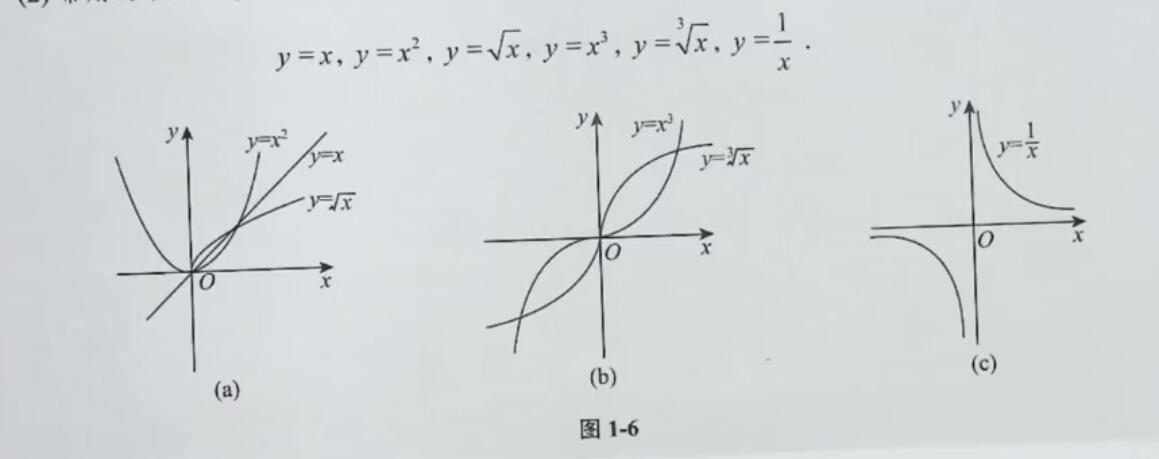
y=xμ
其定义域与值域取决于μ的值,当x>0时,y=xμ都有定义
常用的幂函数:
提示
当x>0时,由y=x, y=x, y=3x, y=lnx具有相同的单调性,与y=x1具有相反的单调性,故:
见到u、 3u时,可用u来研究最值
※ 见到∣u∣时,由∣u∣=u2,可用u2来研究最值
※ 见到u1u2u3时,可用ln(u1u2u3)=lnu1+lnu2+lnu3来研究最值
见到u1时,可用u来研究最值(结论相反)
y=ax(a>0,a=1)
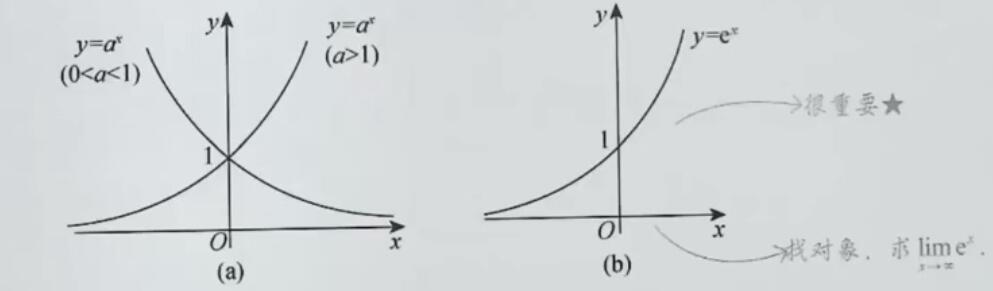
定义域:(−∞,+∞),值域:(0,+∞)
单调性:当a>1时,y=ax单调增加;当0<a<1时,y=ax单调减少
常用的指数函数:y=ex
极限:
x→−∞limex=0,x→∞limex=+∞
但是
x→∞limex不存在
提示
函数极限具有唯一性
只要有多个极限答案,就填不存在
特殊函数值:a0=1,e0=1
指数运算法则:
aα⋅aβ=aα+β,aβaα=aα−β,(aα)β=aαβ,(ab)α=aα⋅bα,(ba)α=bαaα
如:etanx−esinx=esinx(etanx−sinx−1)
y=logax(a>0,a=1),是y=ax的反函数
当a=e时,称为自然对数(lnx)
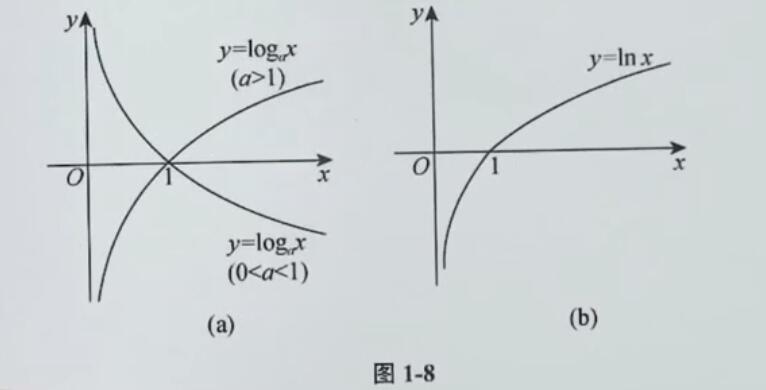
定义域:(0,+∞),值域:(−∞,+∞)
单调性:当a>1时,单增;当0<a<1时,单减
常用的对数函数:y=lnx(e=2.718...)
特殊函数值:loga1=0,logaa=1,ln1=0,lne=1
极限:
x→0+limlnx=−∞,x→+∞limlnx=+∞
统一化思想 技巧
ln(e+x1)−1=ln(e+x1)−lne=ln(1+ex1)
常用公式
x=elnx(x>0),uv=elnuv=evlnu
对数运算法则
loga(MN)=logaM+logaN
logaNM=logaM−logaN
logaMn=nlogaM
loganM=n1logaM
常考:当x>0时:
lnx=21lnx;lnx1=−lnx;ln(1+x1)=lnxx+1=ln(x+1)−lnx
①. 正弦函数与余弦函数
正弦函数y=sinx,余弦函数y=cosx
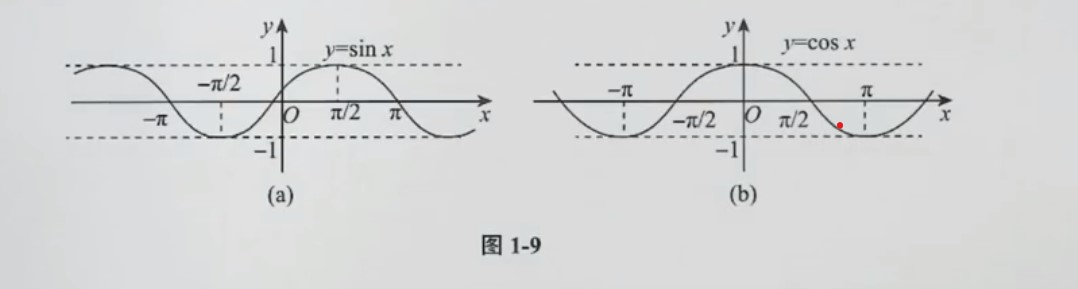
关于图像面积
"一拱"的面积为2 把一拱分为四等分时,外侧两半面积为1−22,内测两半面积为22
定义域:(−∞,+∞)
值域:[1−,1]
奇偶性、周期性(2π为最小正周期)
有界性:∣sinx∣≤1,∣cosx∣≤1
注意当x→0+时,sinx<x
特殊函数值:(不用说了吧)
特殊值:sin2a+cos2a=1
②. 正切函数与余弦函数
正切函数:y=tanx=cosxsinx,余切函数y=cotx=tanx1
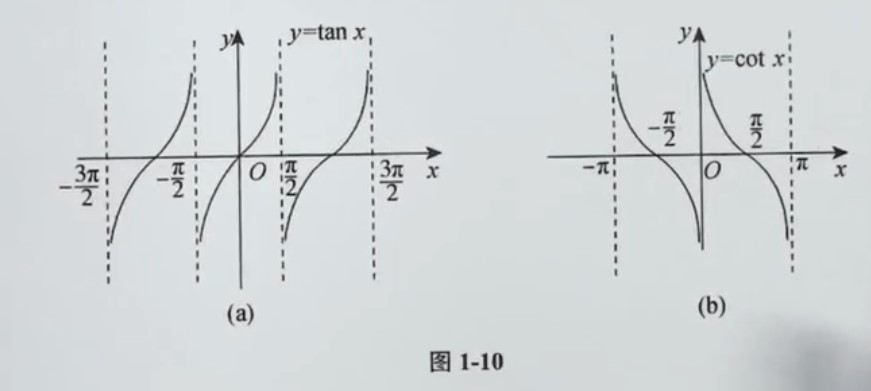
| 函数 | y=tanx | y=cotx |
|---|
| 定义域 | {x∣x∣=kπ+2π} | {x∣x∣=kπ} |
| 值域 | (−∞,+∞) | (−∞,+∞) |
| 奇偶性 | 奇函数 | 奇函数 |
| 最小正周期 | π | π |
③. 正割函数与余割函数
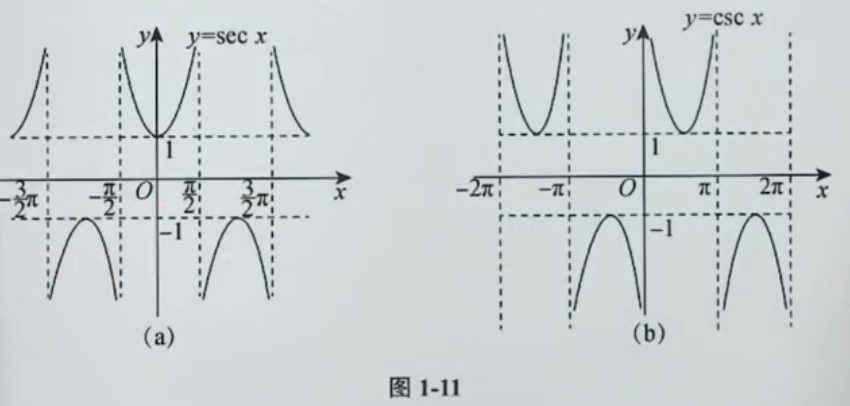
正割函数:y=secx=cox1,余割函数y=cscx=sinx1
巧记
secx以s开头,是另一个cosx的倒数
cscx以c开头,是另一个sinx的倒数
| 函数 | y=secx | y=cscx |
|---|
| 定义域 | {x∣x∣=kπ+2π} | {x∣x∣=kπ} |
| 值域 | (−∞,−1]∪[1,+∞) | (−∞,−1]∪[1,+∞) |
| 奇偶性 | 偶函数 | 奇函数 |
| 最小正周期 | 2π | 2π |
特殊公式
※ 1+tan2a=sec2a;1+cot2a=csc2a
①. 反正弦函数与反余弦函数
反正弦函数y=arcsinx,反余弦函数y=arccosx
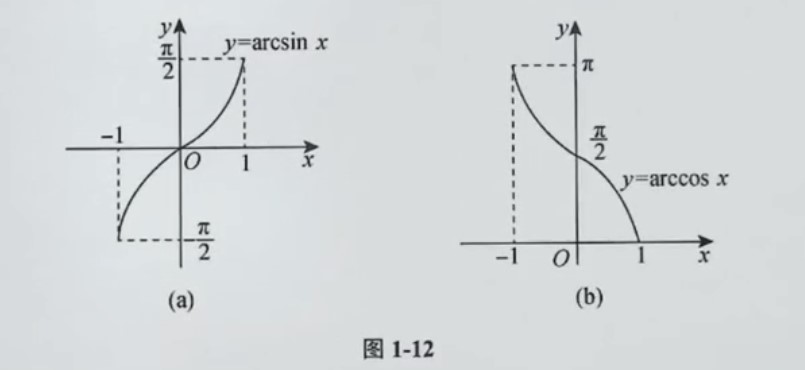
y=arcsinx是y=sinx(−2π≤x≤2π)的反函数
y=arccosx是y=cosx(0≤x≤π)的反函数
主值区间(值域):
y=arcsinx的主值区间为[−2π,2π]
y=arccosx的主值区间为[0,π]
反三角函数的恒等式:


②.反正切函数与反余切函数
反正切函数y=arctanx,反余切函数y=arccotx
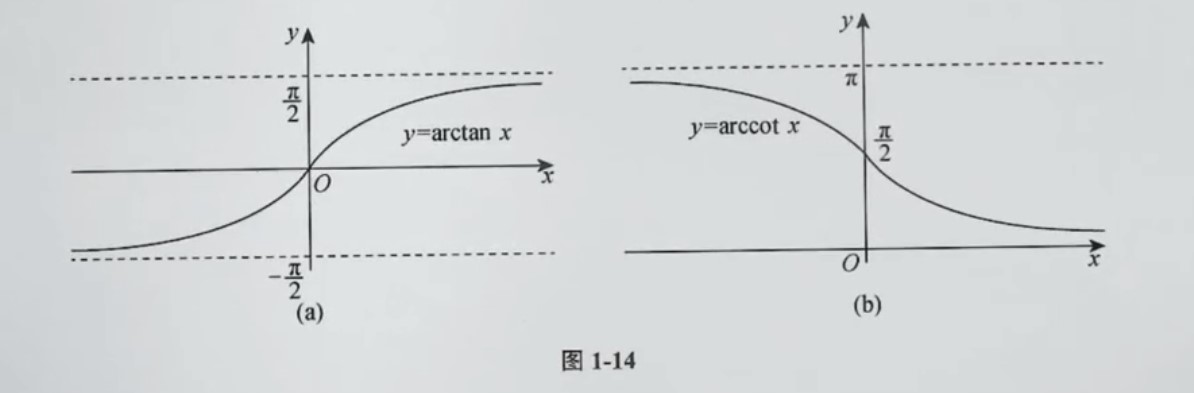
arctanx单增,arccotx单减
定义域:(−∞,+∞)
值域:y=arctanx 的值域为 (−2π,2π), y=arccotx的值域为(0,π)
单调性:y=arctanx单增,y=arccotx单减
奇偶性:y=arctanx为奇函数(在其定义域内)
有界性:两个函数在其定义域内均有界
性质:arctanx+arccotx=2π
※ 特殊函数值:
| x | arctanx | arccotx |
|---|
| 0 | 0 | 2π |
| 3π | 6π | 3π |
| 1 | 4π | 4π |
| 3 | 3π | 6π |
极限:略
由以上基本初等函数经过有限次的四则运算,以及有限次的复合步骤后所构成的,并且可以由一个式子所表示的函数,称为初等函数
初等函数的定义域可以是一个区间,也可以是几个区间的并集,甚至可以是几个孤立的点...
幂指函数u(x)v(x)也是初等函数,当x>0时,f(x)=xx=exlnx是初等函数
注意这个式子!!之后会经常用到!!
在自变量的不同变化范围中,对应法则用不同式子来表示的函数称为分段函数
分段函数不是初等函数,因为它是由多个式子所构成的
分段函数的典型形式如下:
f(x)=⎩⎨⎧φ1(x),a,φ2(x),x>x0x=x0x<x0
下面列出三个比较重要的分段函数:
① y=∣x∣=⎩⎨⎧x,−x,x>0x<0 称为绝对值函数
② y=sgnx=⎩⎨⎧1,0,−1,x>0x=0x<0 称为符号函数。对于任意实数x,有x=∣x∣sgnx
③ y=[x]称为取整函数
定义:设x为任一实数,不超过x的最大整数称为x的整数部分
即:x−1<[x]≤x
注意负数的取整
取整函数的定义域为R,值域为Z
特别地,有:
① [x+n]=[x]+n
② limx→0+[x]=0;limx→0−[x]=−1











